Regression
Regression in machine learning is commonly considered to be a type of supervised learning technique where the output is a real or continuous value. Examples of regression problems include predicting house prices, stock prices, height, weight, and many more. The goal of regression is to create a mathematical model that can help predict a quantitative output.
Types of Regression
Regression problems are either Simple Regression, one independent variable and one dependent variable, and Multiple Regression where there are more than one independent variables and one dependent variable.
Among the several types of regression techniques available to make predictions, the number of independent variables, the type of dependent variables, and the shape of the regression line are the differentiating factors.
Linear Regression:
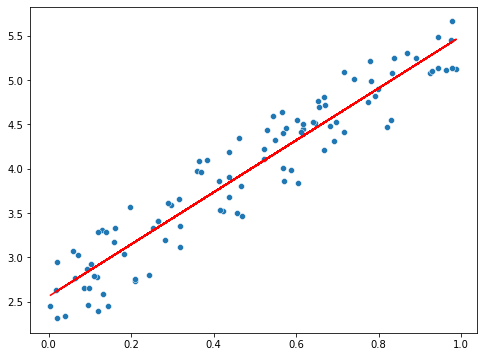
Linear regression is one of the most well-known algorithms in machine learning and statistics. It is an error to assume that the input-ouput relation is linear or an affine transformation. Linear regression is a fundamental algorithm in machine learning and statistics. It assumes a linear relationship between the input variables (also known as independent variables or predictors) and the output variable (also known as the dependent variable or response). The regression function is used to estimate the parameters of this relationship. While linear regression can handle relationships that are not perfectly linear, it may not perform well if the relationship is highly non-linear. In such cases, other methods like polynomial regression or non-linear regression might be more appropriate.
Polynomial Regression:
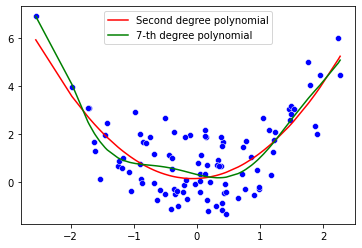
Polynomial regression is a form of regression analysis in which the relationship between the independent variable x and the dependent variable y is modelled as an nth degree polynomial, i.e. it is not linear. However, polynomial regression is linear regression contrary to common misconception. The reason is that the coefficient have a linear relationship to the input variables. Once the model has been fit, the coefficients are just numbers that are multiplied and added linearly to the input variables.
So when one say linear regression all that matters is the relation of the coefficients to the input and output variables, not to other coefficients.
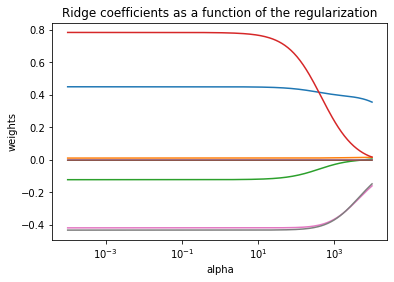
Ridge Regression:
Ridge regression, also known as Tikhonov regularization, is a sophisticated statistical technique that is primarily used in the estimation of multiple-regression model coefficients, particularly in situations where independent variables exhibit a high degree of correlation. This method is an extension of linear regression, a common statistical analysis technique. The main issue with linear regression is that it tends to produce unstable estimates of parameters when multicollinearity is present, i.e., when independent variables are highly correlated. This is where Ridge regression comes into play. It introduces a degree of bias into the regression estimates, which can lead to more reliable and interpretable model estimates. The Ridge regression accomplishes this by adding a penalty equivalent to the square of the magnitude of the coefficients. This penalty term, also known as the L2-norm penalty, discourages large coefficients and thus helps to prevent overfitting. The complexity parameter, λ, controls the amount of shrinkage: the larger the value of λ, the greater the amount of shrinkage. This technique is particularly useful in applications where prediction accuracy is more important than interpretation.
Simple linear regression and Ridge regression are both analytical techniques for examining multiple variables and their relationships. In comparison, simple linear regression struggles with multicollinearity and can lead to overfitting, especially with many predictor variables. Ridge regression manages these issues by introducing bias into the regression estimates and adding a penalty term to the loss function. Moreoever, coefficient estimation in simple linear regression is achieved by minimizing the sum of squared residuals, while Ridge regression does this by also considering the squared magnitude of the coefficients. Although simple linear regression models are generally easier to interpret, Ridge regression can often provide better predictive accuracy.
Lasso Regression:
Lasso regression, also known as Least Absolute Shrinkage and Selection Operator regression, is a specific kind of linear regression, a common statistical data analysis technique. What sets Lasso regression apart is its unique use of a process called shrinkage. This process is particularly beneficial in certain situations because it tends to favor solutions that have fewer non-zero coefficients. In simpler terms, it means that Lasso regression tends to rely on a smaller number of input features to predict the output. This effectively simplifies the model, making it easier to interpret and reducing the risk of overfitting, which is when a model is too closely tailored to the training data and performs poorly on new, unseen data.
ElasticNet Regression:
ElasticNet is a type of linear regression model, which is a popular statistical technique for predicting a real-valued output based on one or more input features. What makes ElasticNet special is that it combines two different types of regularization, known as l1 and l2, to train the model. Regularization is a technique used to prevent overfitting by adding a penalty to the loss function, which is what the model tries to minimize.
The l1 regularization, also known as Lasso, encourages the model to use only a sparse subset of the available features, meaning it makes some of the weight coefficients zero. This is useful when we believe many of the input features may not be relevant. On the other hand, the l2 regularization, also known as Ridge, doesn't result in elimination of coefficients but effectively reduces their values, thus distributing the weights more evenly. This is beneficial when we believe all input features contribute to the output. By combining these two types of regularization, ElasticNet can enjoy the benefits of both, making it a versatile tool for many predictive modeling tasks.
Regression Algorithms
Some of the most important regression algorithms are:
- Ordinary Least Squares Regression (OLSR)
- Linear Regression
- Stepwise Regression
- Multivariate Adaptive Regression Splines (MARS)
- Locally Estimated Scatterplot Smoothing (LOESS)
- Jackknife Regression